Elektronen in Atomen

Interferenz

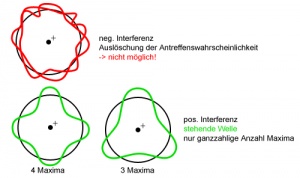
Elektronen in Atomen müssen als Wellen interpretiert werden, die mit sich selber interferieren. Interferenz entsteht, wenn zwei oder mehr Wellen aufeinander treffen. Die Interferenz beschreibt die entstehende Überlagerungserscheinung, das so genannte Interferenzmuster. Grundsätzlich können zwei Typen unterschieden werden. Das Ganze wird genauer im Wiki-Artikel Das unfassbare Elektron erläutert.

Elektronen in Atomen

Wie die Wahrscheinlichkeitswellen mit sich selbst interferieren

In Atomen kommen die Elektronen als "gefangene Wellen" vor. Das heisst, dass sie mit sich selbst positiv interferieren und so eine stehende Welle bilden, denn nur stehende Wellen mit positiver Interferenz bilden einen stabilen Zustand. Bei negativer Interferenz würde ein instabiler Zustand entstehen, welcher das Elektron nicht einnehmen kann - es würde nicht mehr existieren, da sich die negativ interferierenden Wellen auflösen würden. Je weiter das Elektron vom Atomkern entfernt ist (höhere potentielle Energie) desto kleiner ist die Wellenlänge (aufgrund der höheren Energie). Je kleiner die Wellenlänge ist desto höher ist die Anzahl Maxima (bzw. Nullstellen). Damit eine stehende Welle gebildet werden kann, ist nur eine ganzzahlige Anzahl Maxima möglich. Das bedeutet, dass sich die Elektronen nur in bestimmten Abständen zum Kern aufhalten können. Diese Aufenthaltsräume heissen Orbitale. Der kleinstmögliche Abstand entspricht der K-Schale. Dort schwingt die Welle mit ihrer Grundschwingung. Bei der L-Schale hat sie einen Knotenpunkt. Durch diesen schalenartigen Aufbau lassen sich verschiedene Phänomene wie z.B. die Flammenfarben (beim Verbrennen verschiedener Metalle) oder fluoreszierende Gegenstände erklären.

Stehende Welle

Als stehende oder gefangene Welle bezeichnet man eine Welle, welche Punkte (Nullpunkte oder Knotenpunkte: unten rot dargestellt) hat, die sich nicht bewegen.

Gefangene Wellen entstehen, wenn eine Welle z.B. an einer Wand reflektiert wird und dann positiv mit sich selbst interferiert. Wenn daraus keine positive Interferenz resultieren würde, würden keine Knotenpunkte entstehen und das Ganze wäre keine stehende Welle. Da das Elektron einer stehenden 3D-Welle entspricht und dies schwer vorstellbar ist, werden zunächst die einfacheren stehenden 1D- und 2D-Wellen dargestellt:

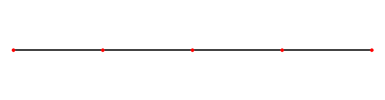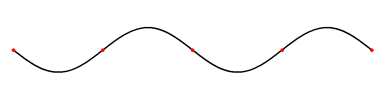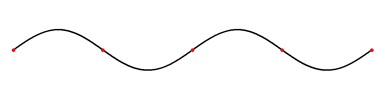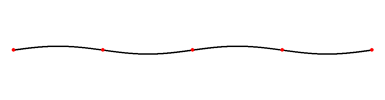
Eindimensionale stehende Welle

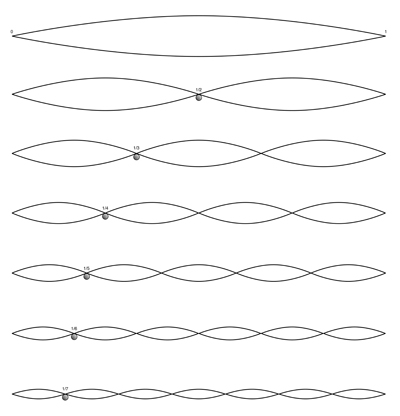
Eine eindimensionale stehende Welle besteht aus einer Strecke (eindimensional), welche in einer Ebene (zweidimensional) schwingt. Eine stehende Welle hat immer mindestens zwei Knotenpunkte am Anfang und am Ende. Die sogenannte "Grundschwingung" ist die stehende Welle, bei der die grösste Wellenlänge erreicht wird. Die weiteren stehenden Wellen sind die so genannten „Oberschwingungen“ der Grundschwingung. Auf das Elektron bezogen, würde das bedeuten, dass sich das Elektron nur auf der Strecke zwischen den beiden Endpunkten bewegen kann. Die Amplitude gibt nur die Wahrscheinlichkeit am jeweiligen Ort an.

Gitarre und Obertöne

Eine Gitarre hat verschiedene Saiten, die beim Spielen zum Schwingen gebracht werden. Jede Saite hat eine gewisse Grundschwingung. Wenn man jedoch die Wellenlänge der Saiten verkürzt, werden andere Schwingungen und dadurch auch andere Töne erzeugt. Dies gelingt allerdings nur dann, wenn eine positive Interferenz vorhanden ist. In der Musik werden so die verschiedenen Intervalle definiert.

• Eine Oktave z.B. entsteht bei der Halbierung der Wellenlänge.
• Beim Verhältnis 2:3 entsteht eine Quinte.
• Beim Verhältnis 3:4 entsteht eine Quarte.

Allerdings hört man nicht nur einen Ton, wenn man eine Seite in Schwingung versetzt, sondern auch noch verschiedene "Obertöne", die auch entstehen. Ein Oberton entsteht nämlich dann, wenn eine Schwingung vorhanden ist, die mit einem ganzzahligen Vielfachen der Frequenz der Grundschwingung bzw. des Grundtons schwingt.

Zweidimensionale stehende Welle

Eine zweidimensionale stehende Welle besteht aus einer Ebene (zweidimensional), welche in einem Raum (dreidimensional) schwingt. Bei der zweidimensionalen stehenden Welle gibt es „Knotenstrecken“ (in der Skizze rot eingezeichnet), nicht nur Knotenpunkte. Auf das Elektron bezogen, würde das bedeuten, dass sich das Elektron nur auf der Ebene bewegen kann. Die Amplitude (Höhe) gibt die Antreff-Wahrscheinlichkeit am jeweiligen Ort an.

Chladnische Klangfiguren

"Chladnische Klangfiguren nennt man die Muster, die entstehen, wenn man eine mit Sand bestreute, dünne Platte (bevorzugt aus Metall) in Schwingungen versetzt. Dies kann man z.B. mit einer Stimmgabel oder mit einem Geigenbogen machen. Nun wird der Sand, den man vorhin auf der Platte verteilt hat, an den Stellen, wo die Platte stark schwingt, weggeschleudert und lagert sich dort ab, wo die Platte nicht oder nur schwach schwingt - genau da befinden sich die Knotenlinien der stehenden Wellen.

[1] - Link zu einem Bild (zur Veranschaulichung)

Hier sieht man, wie die Chladnischen Klangfiguren bei quadratischen Platten aussehen.

Dreidimensionale stehende Welle

Theoretisch müsste eine zweidimensionale stehende Welle aus einem Raum (dreidimensional), welcher in einem vierdimensionalen Gebilde schwingt, bestehen. Es gibt "Knotenräume" und nicht "Knotenstrecken" bzw. "-punkte". Dies kann man sich jedoch nicht vorstellen, da wir nur drei Dimsenionen wahrnehmen.

Orbitale

Elektronen sind dreidimensionale stehende Wahrscheinlichkeitswellen. Für jeden Punkt im Raum gibt es so eine bestimmte Wahrscheinlichkeit das Elektron anzutreffen. Diese Wahrscheinlichkeiten können berechnet werden. Dazu braucht man die so genannten Schrödingergleichungen, womit man die folgenden zwei Komponenten auf sehr komplizierte Weise berechnen kann.

1. Energetische Komponente: Der Abstand zum Kern (Anzahl Nullstellen ist proportional zur Energie) eines Elektrons nennt man das Energieniveau des Elektrons
2. Räumliche Komponente: „Antreffenswahrscheinlichkeitsraum“ = Orbital (der Teil des Raumes, in dem man mit grosser Wahrscheinlichkeit das Elektron antreffen wird).

Mehr zu den Orbitalen erfahrt ihr im Artikel Orbitale.

Quellen

• Chemienotizen
• Powerpoint-Präsentationen von Herrn Deuber - zu finden im BSCW
• [2] - Englischer Artikel zu den Obertönen
• [3] - Deutscher Artikel zu den Chladnischen Klangfiguren