Elektronen in Atomen

Interferenz

Elektronen in Atomen müssen als Wellen interpretiert werden, die mit sich selber Interferenz machen. Interferenz entsteht, wenn zwei (oder mehr) Wellen aufeinander treffen. Die Interferenz beschreibt die entstehende Überlagerungserscheinung, das so genannte Interferenzmuster. Grundsätzlich können zwei Typen unterschieden werden:

positive Interferenz

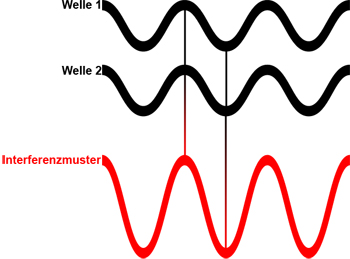
Die erste Möglichkeit der Interferenz ist die so genannte positive oder konstruktive Interferenz. Sie tritt auf, wenn die zwei aufeinandertreffenden Wellen in Phase (die selbe Wellenlänge und am gleichen Ort Maxima bzw. Minima) sind. Die positive Interferenz erzeugt eine verstärkte Welle. Siehe Darstellung unten.

negative Interferenz

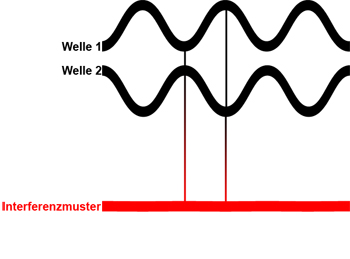
Eine weitere Möglichkeit ist die negative oder destruktive Interferenz. Die Wellen sind in Gegenphase (gleiche Wellenlänge aber Maxima und Minima genau um eine halbe Wellenlänge verschoben). Die negative Interferenz erzeugt eine Auslöschung der Welle. Siehe Darstellung unten.

Interferenz im Alltag

Beispiel: Regenbogenfarben auf Seifenblasenhaut: Licht verschiedener Farben hat bekanntlich verschiedene Wellenlängen.

Skizze zur Interferenz von Licht an der Seifenblasenhaut

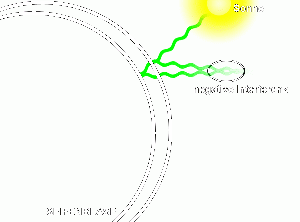
Jeder Lichtstrahl wird bei der Seifenblasenhaut zwei Mal gebrochen (siehe Skizze). Da bei diesen beiden Brechungen der Winkel nicht genau übereinstimmt, treffen die Lichtstrahlen ausserhalb der Seifenblase wieder aufeinander, wo so gezwungenermassen eine Interferenz stattfindet. Wenn nun bei einem bestimmten Abschnitt auf der Seifenblase eine bestimmte Farbe ausgelöscht (durch negative Interferenz) wird, so erscheint der entsprechende Abschnitt in der Komplementärfarbe. Andere Beispiele, bei denen derselbe Vorgang eine Rolle spielt:

• Ölschicht
• Insekten (Flügel oder Panzer)
• CD

Welle-Teilchen-Dualismus

Wenn man Elektronen beobachtet, merkt man, dass sie:

• Wellen (Wahrscheinlichkeitswellen) sind, wenn der Aufenthaltsort nicht genau bestimmt ist.
• Teilchen sind, wenn der Aufenthaltsort bestimmt wird.

Normalerweise ist jedes Physikalische Experiment reproduzierbar. Bei den Elektronen als Teilchen ist dies jedoch nicht so. Das heisst, dass das genau selbe Experiment verschiede Ergebnisse haben kann. Als Beispiel kann man 2 Mal ein Elektron mit genau gleichen Bedingungen auf eine Fläche schiessen und trotzdem erhält man bei den beiden Versuchen verschiede Ergebnisse. Dies hängt mit der Wahrscheinlichkeitsverteilung der Wellengleichung zusammen.

Elektronen in Atomen

Wie die Wahrscheinlichkeitswellen mit sich selbst interferieren

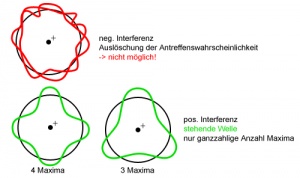
In Atomen kommen die Elektronen als gefangene Wellen vor. Das heisst, dass sie positive Interferenz mit sich selber machen und so eine stehende Welle bilden, denn nur stehende Wellen mit positiver Interferenz bilden einen stabilen Zustand. Bei negativer Interferenz würde ein instabiler Zustand entstehen, welcher das Elektron nicht einnehmen kann. Je weiter entfernt das Elektron vom Kern (höhere potentielle Energie), desto kleiner ist die Wellenlänge (höhere Energie). Je kleiner die Wellenlänge, desto höher ist die Anzahl Maxima (bzw. Nullstellen). Damit eine stehende Welle entstehen kann, ist nur eine ganzzahlige Anzahl Maxima möglich. Das bedeutet, dass sich die Elektronen nur in bestimmten Abständen zum Kern aufhalten können. Diese Aufenthaltsräume heissen Orbitale. Der kleinstmögliche Abstand entspricht der K-Schale. Dort ist die hat die Welle Grundschwingung. Bei der L-Schale hat sie 1 Knotenpunkt. Durch diesen schalenartigen Aufbau lassen sich verschiedene Phänomene wie z.B. die Flammenfarben oder fluoreszierende Gegenstände erklären.

Stehende Welle

Als stehende oder gefangene Welle bezeichnet man eine Welle, welche Punkte (Nullpunkte oder Knotenpunkte: unten rot dargestellt) hat, die sich nicht bewegen

Gefangene Wellen entstehen, wenn eine Welle z.B. an einer Wand reflektiert wird und dann positive Interferenz mit sich selbst macht. Wenn keine positive Interferenz resultieren würde, würden keine Knotenpunkte entstehen und das ganze wäre keine stehende Welle. Da das Elektron einer stehenden 3D-Welle entspricht und dies sehr schwierig zu verstehen ist, werden zunächst die einfacheren stehenden 1D- und 2D-Wellen dargestellt:

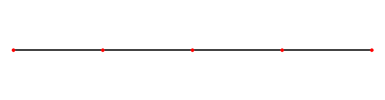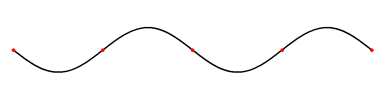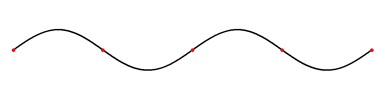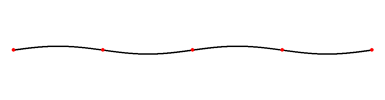
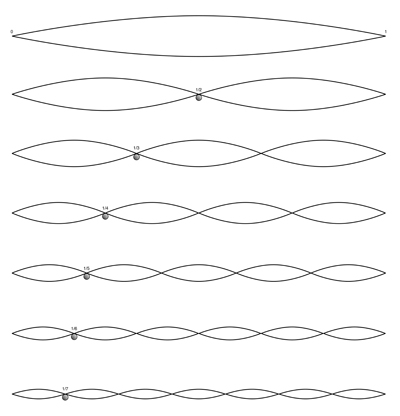
Eindimensionale stehnde Welle

Eine eindimensionale stehende Welle besteht aus einer Strecke (eindimensional), welche in einer Ebene (zweidimensional) schwingt. Eine stehende Welle bedingt immer mindestens 2 Knotenpunkte am Anfang und am Ende. Die sogenannte Grundschwingung ist die stehende Welle, bei der die grösste Wellenlänge erreicht wird. Die weiteren stehenden Wellen sind die so genannten „Oberschwingungen“ der Grundschwingung. Auf das Elektron bezogen, würde das bedeuten, dass sich das Elektron nur auf der Strecke zwischen den beiden Endpunkten bewegen kann. Die Amplitude gibt nur die Wahrscheinlichkeit am jeweiligen Ort an.

zweidimensionale stehende Welle

Eine zweidimensionale stehende Welle besteht aus einer Ebene (zweidimensional), welche in einem Raum (dreidimensional) schwingt. Bei der zweidimensionalen stehenden Welle gibt es „Knotenstrecken“ (in der Skizze rot eingezeichnet), nicht nur Knotenpunkte. Auf das Elektron bezogen, würde das bedeuten, dass sich dsa Elektron nur auf der Ebene bewegen kann. Die Amplitude (Höhe) gibt die Antreffenswahrscheinlichkeit am jeweiligen Ort an.

dreidimensionale stehende Welle

Theoretisch müsste eine zweidimensionale stehende Welle aus einem Raum (dreidimensional), welcher in einem vierdimensionalen Gebilde schwingt bestehen. Wie soll man sich das vorstellen? Wie kann man das darstellen?

Orbitale

Elektronen sind dreidimensionale stehende Wahrscheinlichkeitswellen. Für jeden Punkt im Raum gibt es so eine bestimmte Wahrscheinlichkeit das Elektron anzutreffen. Diese Wahrscheinlichkeiten können berechnet werden. Dazu braucht man die so genannten Schrödingergleichungen, womit man die folgenden zwei Komponenten auf sehr komplizierte Weise berechnen kann. 1. Energetische Komponente: Abstand zum Kern (Anzahl Nullstellen ist proportional zur Energie) 2. Räumliche Komponente: „Antreffenswahrscheinlichkeitsraum“ = Orbital