Das unfassbare Elektron: Unterschied zwischen den Versionen
Ganflo (Diskussion | Beiträge) |
Ganflo (Diskussion | Beiträge) |
||
| Zeile 42: | Zeile 42: | ||
== Unfassbar == | == Unfassbar == | ||
| − | + | ===In der klassischen Physik=== | |
Was macht das Elektron so unfassbar? Bis heute ist man mit der Technik noch nicht im Stande, den Ort und die Geschwindigkeit gleichzeitig zu betimmen. Denn man hat herausgefunden, sobald man den einen Faktor genauer feststellt, wird der andere Faktor ungenauer. Das wird alles durch die Unschärferelationstheorie, die 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert wurde,erklärt. | Was macht das Elektron so unfassbar? Bis heute ist man mit der Technik noch nicht im Stande, den Ort und die Geschwindigkeit gleichzeitig zu betimmen. Denn man hat herausgefunden, sobald man den einen Faktor genauer feststellt, wird der andere Faktor ungenauer. Das wird alles durch die Unschärferelationstheorie, die 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert wurde,erklärt. | ||
| − | + | ????===∆p*∆q~h=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ''∆p = Unschärfe der Geschwindigkeit (Impuls); | ||
| + | ∆q = Unschärfe des Ortes; | ||
| + | h = "Plancksches Wirkungsquantum'' | ||
| + | '' | ||
| + | Ergibt ein konstantes Ergebnis, bei welchem, wenn man ∆p erhöht, sich ∆q verkleinert und umgekehrt.'' | ||
| + | Den Ort zu bestimmen ist sehr schwer, da sich die Teilchen unglaublich schnell bewegen. Wenn der Ort bestimmt ist, ist das Atom jedoch schon wieder an einem anderen Ort, es bleibt gar keine Zeit um die Geschwindigkeit irgendwie zu messen. | ||
| − | + | ===In der Quantenphysik=== | |
| − | + | ????Es ist möglich beliebig genau die Wahrscheinlichkeit zu berechnen, wie gross die Wahrscheinlichkeit ist, ein Elektron an einem bestimmten Ort anzutreffen. Die Berechnung für die Wahrscheinlichkeit des Antreffens an einem bestimmten Ort des Elektrons kann mittels einer mathematischen Wellengleichungg berechnet werden. | |
== Quellen == | == Quellen == | ||
Version vom 17. April 2010, 14:50 Uhr
Der Name kommt Elektron vom griechischen Wort ηλεκτρόν was soviel bedeutet wie Bernstein, denn an ihm wurde die Elektrizität erstmals beobachtet. Reibt man Bernstein beispielsweise mit einem Katzenfell, so lädt sich das Fell elektrisch auf. 1927 entdeckten Clinton Davisson & Lester Germer bei einem Experimentdie sogennanten Beugungsringe. Das Bedeutet, dass ein Elektorn nicht wirklich als ein Objekt im normalen Sinn betrachtet werden kann sondern eher als eine Welle betrachtet wird.
Inhaltsverzeichnis
Allgemeines
Im Atombau
Elektronen sind negativ geladene Elementarteilchen (e⁻). Das Gegenstück zu den positiv geladenen Protonen (p+).
Im Kern befinden sich die Neutronen (n°) und die Protronen. Sie sind umgeben von dem/den Elektronen. Die Elektronen bilden die Hülle des Atoms. Sie haben keine innere Strukturen und können als Punktförmig angenommen werden. Doch es sind nicht kleine Bällchen, die um den Kern kreisen wie die Planeten um einen Stern. Man muss sich das ganze eher als stehende Materiewelle vorstellen.
Atomhülle
Die Elektronen bewegen sich in den Atomhüllen (= Elektronehülle). Die Anzahl Elektronen entsprciht bei einem ungeladenem (neutralem) Atom der Ordnungszahl oder auch der Anzahl Protonen im Kern.
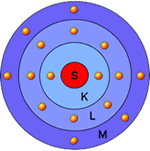
Sind es mehr Elektron so ist es negativ geladen, wenn es mehr Protonen sind positiv. Die Schalen werden von den Elektronen in bestimmter Reihenfolge besetzt, nicht jede Hülle hat die selbe Anzahl an Elektron. Diese wird von den Anziehungskräften bestimmt.
Unfassbar
In der klassischen Physik
Was macht das Elektron so unfassbar? Bis heute ist man mit der Technik noch nicht im Stande, den Ort und die Geschwindigkeit gleichzeitig zu betimmen. Denn man hat herausgefunden, sobald man den einen Faktor genauer feststellt, wird der andere Faktor ungenauer. Das wird alles durch die Unschärferelationstheorie, die 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert wurde,erklärt.
????===∆p*∆q~h===
∆p = Unschärfe der Geschwindigkeit (Impuls);
∆q = Unschärfe des Ortes;
h = "Plancksches Wirkungsquantum
Ergibt ein konstantes Ergebnis, bei welchem, wenn man ∆p erhöht, sich ∆q verkleinert und umgekehrt.
Den Ort zu bestimmen ist sehr schwer, da sich die Teilchen unglaublich schnell bewegen. Wenn der Ort bestimmt ist, ist das Atom jedoch schon wieder an einem anderen Ort, es bleibt gar keine Zeit um die Geschwindigkeit irgendwie zu messen.
In der Quantenphysik
????Es ist möglich beliebig genau die Wahrscheinlichkeit zu berechnen, wie gross die Wahrscheinlichkeit ist, ein Elektron an einem bestimmten Ort anzutreffen. Die Berechnung für die Wahrscheinlichkeit des Antreffens an einem bestimmten Ort des Elektrons kann mittels einer mathematischen Wellengleichungg berechnet werden.
Quellen
- Chemieunterlagen
- Wikipedia
