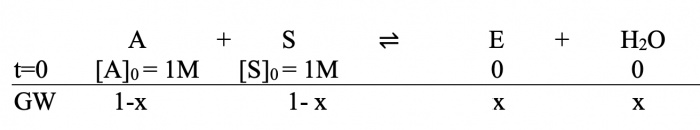Die Berechnung von Gleichgewichtskonzentrationen: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
Gesucht ist [E]GW also [E] im Gleichgewichtszustand, wobei K=4 sei. | Gesucht ist [E]GW also [E] im Gleichgewichtszustand, wobei K=4 sei. | ||
| − | + | Wir setzen nun die gesuchte [E]GW als x, entsprechend werden die Edukte im GW zu 1-x: | |
Lösungsweg: | Lösungsweg: | ||
| Zeile 39: | Zeile 39: | ||
[[Datei:rechenweg.jpg|700px]] | [[Datei:rechenweg.jpg|700px]] | ||
| − | + | Die Lösung ist also x1, da es keine Minuskonzentrationen gibt | |
x1 = 2/3 → [E]GW = 2/3 Mol (ca. 0.667 Mol) | x1 = 2/3 → [E]GW = 2/3 Mol (ca. 0.667 Mol) | ||
Version vom 26. Dezember 2021, 23:08 Uhr
Einführung: Bedeutung von K
Die Gleichgewichtskonstante K gibt ein Verhältnis von Mengen der bei einer chemischen Reaktion beteiligten Stoffe wieder. Liegen die Edukte und Produkte der Reaktion in dem durch die Gleichgewichtskonstante gegebenen Verhältnis vor, so befindet sich die Reaktion im chemischen Gleichgewicht. Dann findet kein Nettofluss durch die Reaktion statt.
Der Fluss durch die Hinreaktion ist gleich dem Fluss durch die Rückreaktion!
Kennt man also K, so kann man Aussagen über die Lage des Gleichgewichts einer Reaktion machen. Wir wissen dann, ob eine Reaktion überhaupt abläuft, die Produktekonzentration überwiegt, das Gleichgewicht in der Mitte ist, oder ob allenfalls die Edukte überwiegen.
Die Berechnung an einem Beispiel
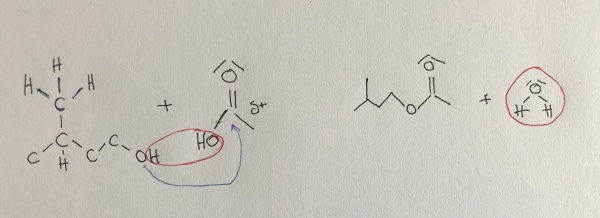
Synthese von Bananenesther
3-Methyl-butanol + Essigsäure ⇌ Essigsäure-3-methyl-butyl-ester + Wasser
(Die Hydroxylgruppe verbindet
sich mit der Essigsäure)
Berechnung:
Die anfänglichen Edukte sind also gegeben (die Produkte am Anfang noch 0). Gesucht ist [E]GW also [E] im Gleichgewichtszustand, wobei K=4 sei.
Wir setzen nun die gesuchte [E]GW als x, entsprechend werden die Edukte im GW zu 1-x:
Lösungsweg:
Nun setzen wir in MWG ein:
Die Lösung ist also x1, da es keine Minuskonzentrationen gibt
x1 = 2/3 → [E]GW = 2/3 Mol (ca. 0.667 Mol)
[H2O]GW = 2/3 Mol (ca. 0.667 Mol)
[S]GW & [A]GW = 1/3 Mol (ca. 0.333 Mol)
Ausbeute: Hergestellte Menge : Maximal mögliche Menge = 0.667 M : 1M = 66,7%
Variante: nimmt man [S]0 = 2M, so wird x1= 0.84 x2= 3.15 (wieder nicht möglich)
Dann wäre: → [E]GW = 0.84 M → und die Ausbeute 84%