Das unfassbare Elektron

Der Name Elektron kommt vom griechischen Wort ηλεκτρόν was soviel bedeutet wie Bernstein, denn an ihm wurde die Elektrizität erstmals beobachtet.

grafische Darstellung der Wahrnehmung mit offenen/geschlossenen Augen

Reibt man Bernstein beispielsweise mit einem Katzenfell, so lädt sich das Fell elektrisch auf. 1927 entdeckten Clinton Davisson & Lester Germer bei einem Experiment (siehe unten) die sogennanten Beugungsringe. Das Bedeutet, dass ein Elektorn nicht wirklich als ein Objekt im normalen Sinn betrachtet werden kann sondern eher als eine Welle. Das kann man sich so vorstellen: Wenn man die Augen offen hat, wird das Elektron als ein Teilchen betrachtet. Schliesst man jedoch die Augen, ist das Elektron eine Welle.

Unfassbar

Heisenberg und die Gleichung der Unschärferelation auf einer deutschen Briefmarke

In der klassischen Physik

Was macht das Elektron so unfassbar? Bis heute ist man mit der Technik noch nicht im Stande, den Ort und die Geschwindigkeit gleichzeitig zu betimmen. Denn man hat herausgefunden, sobald man den einen Faktor genauer feststellt, wird der andere Faktor ungenauer. Das wird alles durch die Unschärferelationstheorie, die 1927 von Werner Heisenberg im Rahmen der Quantenmechanik formuliert wurde,erklärt.

∆p*∆q~h

∆p = Unschärfe der Geschwindigkeit (Impuls); ∆q = Unschärfe des Ortes; h = "Plancksches Wirkungsquantum

Ergibt ein konstantes Ergebnis, bei welchem, wenn man ∆p erhöht, sich ∆q verkleinert und umgekehrt.

In der Quantenphysik

Wahrscheinlichkeitswelle mittels Quantenphysik das Elektron anzutreffen

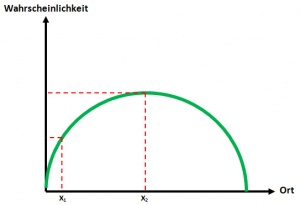
Es ist möglich beliebig genau die Wahrscheinlichkeit zu berechnen, ein Elektron an einem bestimmten Ort anzutreffen. Die Berechnung für die Wahrscheinlichkeit des Antreffens an einem bestimmten Ort des Elektrons kann mittels einer mathematischen Wellengleichungg berechnet werden.

Zur Grafik: bei x1 ist die Wahrscheinlichkeit geringer als bei x2 das Elektron anzutreffen.

Fazit

In der Klassischen Physik ist es unmöglich von einem Elektron den Ort und die Geschwindigketi gleichzeitig zu bestimmen. Somit versagt die Klassische Physik. Hingegen bei der Quantenphysik kann man die Wahrscheinlichkeit des Antreffens berechnen und somit erhält man eine Wellenartige Funktion.

Entdeckung des Wellencharakters

Clinton Davisson (links) und Lester Halbert Germer (rechts)

Die beiden Wissenschaftler Clinton Davisson und Lester Germer entdeckten während einem Experiment ungewollt die Welleneigenschaft der Elektronen. Ihr ursprüngliches Ziel war eigentlich, eine Messmethodik herauszufinden, um die Qualität einer Metalloberfläche zu bestimmen.

Interferenz

Elektronen in Atomen müssen als Wellen interpretiert werden, die mit sich selber Interferenz machen. Interferenz entsteht, wenn zwei (oder mehr) Wellen aufeinander treffen. Die Interferenz beschreibt die entstehende Überlagerungserscheinung, das so genannte Interferenzmuster. Grundsätzlich können zwei Typen unterschieden werden:

positive Interferenz

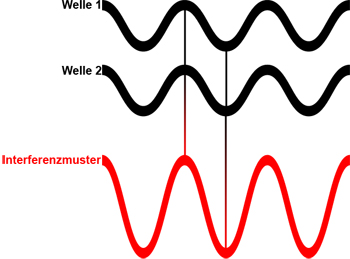
Die erste Möglichkeit der Interferenz ist die so genannte positive oder konstruktive Interferenz. Sie tritt auf, wenn die zwei aufeinandertreffenden Wellen in Phase (die selbe Wellenlänge und am gleichen Ort Maxima bzw. Minima) sind. Die positive Interferenz erzeugt eine verstärkte Welle. Siehe Darstellung unten.

negative Interferenz

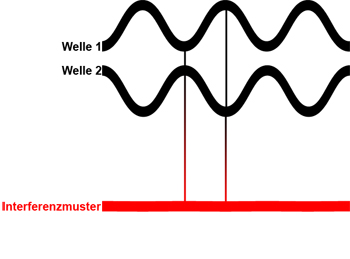
Eine weitere Möglichkeit ist die negative oder destruktive Interferenz. Die Wellen sind in Gegenphase (gleiche Wellenlänge aber Maxima und Minima genau um eine halbe Wellenlänge verschoben). Die negative Interferenz erzeugt eine Auslöschung der Welle. Siehe Darstellung unten.

Interferenz im Alltag

Beispiel: Regenbogenfarben auf Seifenblasenhaut: Licht verschiedener Farben hat bekanntlich verschiedene Wellenlängen.

Skizze zur Interferenz von Licht an der Seifenblasenhaut

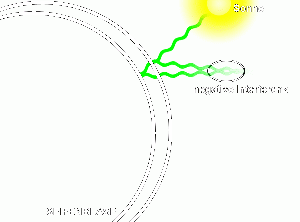
Jeder Lichtstrahl wird bei der Seifenblasenhaut zwei Mal gebrochen (siehe Skizze). Da bei diesen beiden Brechungen der Winkel nicht genau übereinstimmt, treffen die Lichtstrahlen ausserhalb der Seifenblase wieder aufeinander, wo so gezwungenermassen eine Interferenz stattfindet. Wenn nun bei einem bestimmten Abschnitt auf der Seifenblase eine bestimmte Farbe ausgelöscht (durch negative Interferenz) wird, so erscheint der entsprechende Abschnitt in der Komplementärfarbe. Andere Beispiele, bei denen derselbe Vorgang eine Rolle spielt:

• Ölschicht
• Insekten (Flügel oder Panzer)
• CD

Welle-Teilchen-Dualismus

Wenn man Elektronen beobachtet, merkt man, dass sie:

• Wellen (Wahrscheinlichkeitswellen) sind, wenn der Aufenthaltsort nicht genau bestimmt ist.
• Teilchen sind, wenn der Aufenthaltsort bestimmt wird.

Normalerweise ist jedes Physikalische Experiment reproduzierbar. Bei den Elektronen als Teilchen ist dies jedoch nicht so. Das heisst, dass das genau selbe Experiment verschiede Ergebnisse haben kann. Als Beispiel kann man 2 Mal ein Elektron mit genau gleichen Bedingungen auf eine Fläche schiessen und trotzdem erhält man bei den beiden Versuchen verschiede Ergebnisse. Dies hängt mit der Wahrscheinlichkeitsverteilung der Wellengleichung zusammen.

Kommen die Elektornen in einem Atom vor, so muss das Elektron mit sich selbst umbedingt positive Interverenz machen, denn nur dasn ist der Zustand so stabil, dass er bestehen kann.

Quellen

• Chemieunterlagen
• Wikipedia

Weblinks

• [1] Elektron Wikipedia
• [2] Unschärferelation Wikipedia