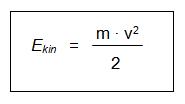Molmasse und Molvolumen: Unterschied zwischen den Versionen
| (17 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[Bild:Eisen + Schwefel.jpg ]] | [[Bild:Eisen + Schwefel.jpg ]] | ||
| + | |||
| + | |||
| + | Das Massenverhältnis gibt vor wie viel Mol Edukten man reagieren lassen soll, damit die Reaktion abläuft. Im obigen Beispiel muss man 1 Mol Eisen mit 1 Mol Schwefel reagieren lassen. Achtung: Produkt ist dann auch 1 Mol und nicht 2 ! | ||
| + | |||
[[Bild:Zentrale_frage.jpg ]] | [[Bild:Zentrale_frage.jpg ]] | ||
| Zeile 18: | Zeile 22: | ||
| − | [[[[Bild: | + | [[[[Bild:Molmasse_Tabelle1.jpg]]]] |
| − | |||
| − | + | Die Zahl 6,02 · 10<sup>23</sup> ist die Avogadro-Zahl. Sie wird mit der Teilchenebene multipliziert, um die sichtbare Ebene zu erhalten. | |
| − | + | : <b> 6,02 · 10<sup>23</sup> (Avogadro-Zahl) Unit entsprechen 1 Gramm </b> | |
| + | Def.: Ein Mol entspricht der Menge eines Stoffs, die N<sub>A</sub> (=Avogadro-Zahl), d.h. 6,02 · 10<sup>23</sup> Teilchen enthält | ||
| − | == | + | 1 mol ist also eine Teilchenanzahl wie z.B. 1 Dutzend = 12 Teilchen. 1 mol = 6,02 · 10<sup>23</sup> (Avogadro-Zahl!)Teilchen |
| − | |||
| + | Def.: Molmasse entspricht einer Stoffmenge, welche 1 Mol Teilchen enthält. Die Einheit der Molmasse ist g/Mol. Die Molmasse entspricht, der in g ausgedrückten Teilchenmasse eines Stoffes. | ||
| − | |||
| − | + | ==Beispiele== | |
| − | + | === Berechnen der Anzahl Teilchen === | |
| − | |||
| − | + | Man geht dabei in drei Schritten vor: | |
'''I''' Bestimmen der Molmasse | '''I''' Bestimmen der Molmasse | ||
| Zeile 51: | Zeile 53: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Bild:Papiertaschentuch..jpg ]] | |
| − | + | Somit wissen wir jetzt, dass in einem Papiertaschentuch '''9.23 * 10<sup>19</sup> Teilchen''' enthalten sind. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Molvolumen == | == Molvolumen == | ||
| Zeile 83: | Zeile 76: | ||
Umrechnung: | Umrechnung: | ||
| − | : V<sub>NB</sub> & | + | [[Bild:Umrechnungsformel.jpg ]] |
| + | |||
| + | |||
| + | : (V<sub>NB</sub> = Volumen bei Normalbedingungen; V<sub>x</sub> = Volumen bei jeweiliger Situation etc.) | ||
| + | |||
| − | : | + | Eine Frage stellt sich aber noch, diese lautet: |
| + | Ist die Anzahl Gasteilchen in einem bestimmten Volumen von der Art der Teilchen (Grösse / Masse) abhängig? | ||
| − | |||
| + | Saubere Überlegung; | ||
| − | + | - Kinetische Gastheorie: | |
| − | + | [[Bild:Ekin.jpg ]] | |
| − | + | Die mittlere kinetische energie hängt von der '''Temperatur (T)''' ab; sie nimmt mit der Temperatur zu. | |
| − | + | Die Summe aller Stösse der Gasteilchen (miteinander und mit der Gefässwand) verursacht den Druck eines Gases. Je grösser die Anzahl Gasteilchen sowie die kinetische Energie der Gasteilchen, umso grösser ist der Druck und damit auch das Volumen. | |
| − | + | Anders gesagt: Ist die Kinetische Energie von diesen Gasteilchen konstant, so ist auch die Temperatur konstant und somit auch der Platzbedarf konstant. | |
: Kinetische Energie = const. ⇒ Temperatur = const. ⇒ Platzbedarf = const. | : Kinetische Energie = const. ⇒ Temperatur = const. ⇒ Platzbedarf = const. | ||
| + | |||
In Worten gefasst kann man also sagen, dass Teilchen mit kleiner Masse zwar winziger sind, doch durch ihre erhöhte Geschwindigkeit gleich viel Platz brauchen als grosse Teilchen, welche sich langsamer fortbewegen und durch ihre Masse den gleichen Bedarf an Platz decken. | In Worten gefasst kann man also sagen, dass Teilchen mit kleiner Masse zwar winziger sind, doch durch ihre erhöhte Geschwindigkeit gleich viel Platz brauchen als grosse Teilchen, welche sich langsamer fortbewegen und durch ihre Masse den gleichen Bedarf an Platz decken. | ||
| Zeile 108: | Zeile 107: | ||
[[Bild:AVOGADRO.jpg |thumb|right|Amadeo Avogadro; Bild stammt von:[http://www.rsc.org/chemistryworld/Issues/2006/March/Avogadro.asp]]] | [[Bild:AVOGADRO.jpg |thumb|right|Amadeo Avogadro; Bild stammt von:[http://www.rsc.org/chemistryworld/Issues/2006/March/Avogadro.asp]]] | ||
| − | Die vorherige Erkenntnis | + | Die vorherige Erkenntnis stammte von dem italienischen Physiker und Chemiker [[Wikiseite_für_Studierende#Weblinks|Amadeo Avogadro]], der auch die Avogadro-Zahl einführte. Sein Satz lautet wie folgt: |
| Zeile 116: | Zeile 115: | ||
Mit diesem Satz wurden auch die '''Standardbedingungen''' festgelegt, da man jetzt wusste, dass jedes Gas bei gleicher Temperatur und Druck das gleiche Molvolumen haben musste. Die Standardbedingungen setzen voraus, dass die Temperatur bei '''25°C (298 K)''' und der Druck bei '''1013 hPa''' liegen. Bei dieser speziellen Situation beträgt das Molvolumen ≈ '''25l/mol'''. | Mit diesem Satz wurden auch die '''Standardbedingungen''' festgelegt, da man jetzt wusste, dass jedes Gas bei gleicher Temperatur und Druck das gleiche Molvolumen haben musste. Die Standardbedingungen setzen voraus, dass die Temperatur bei '''25°C (298 K)''' und der Druck bei '''1013 hPa''' liegen. Bei dieser speziellen Situation beträgt das Molvolumen ≈ '''25l/mol'''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Experimentelle Bestimmung des Molvolumens === | === Experimentelle Bestimmung des Molvolumens === | ||
Aktuelle Version vom 23. Juni 2010, 15:27 Uhr
Um für bestimmte Reaktionen ausgehend von den Edukten und Produkten die Mengen der einzelnen Stoffe zu berechnen (siehe Chemisches Rechnen), muss man natürlich zuerst wissen, wie man von einer bestimmten Menge eines Stoffes die Anzahl Teilchen berechnen kann. In diesem Kapitel wird beschrieben, wie man mit der Masse bzw. dem Volumen eines Stoffs diese Anzahl berechnen kann. Eine sehr entscheidende Rolle spielt dabei das Mol.
Inhaltsverzeichnis
Molmasse
Experiment: Eisen + Schwefel
Das Massenverhältnis gibt vor wie viel Mol Edukten man reagieren lassen soll, damit die Reaktion abläuft. Im obigen Beispiel muss man 1 Mol Eisen mit 1 Mol Schwefel reagieren lassen. Achtung: Produkt ist dann auch 1 Mol und nicht 2 !
Teilchen sind:
Atome --> Bei Gasen
Ione --> Bei Salzen
Moleküle --> Bei Nichtmetal-Verbindungen
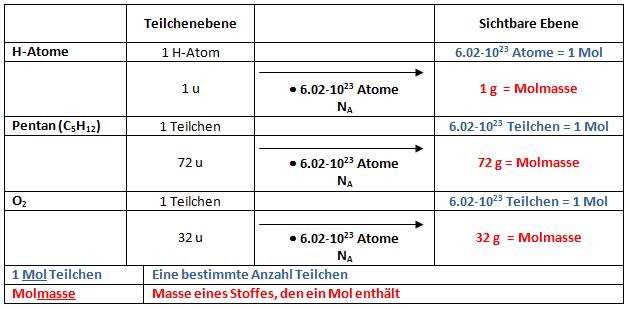
Die Zahl 6,02 · 1023 ist die Avogadro-Zahl. Sie wird mit der Teilchenebene multipliziert, um die sichtbare Ebene zu erhalten.
- 6,02 · 1023 (Avogadro-Zahl) Unit entsprechen 1 Gramm
Def.: Ein Mol entspricht der Menge eines Stoffs, die NA (=Avogadro-Zahl), d.h. 6,02 · 1023 Teilchen enthält
1 mol ist also eine Teilchenanzahl wie z.B. 1 Dutzend = 12 Teilchen. 1 mol = 6,02 · 1023 (Avogadro-Zahl!)Teilchen
Def.: Molmasse entspricht einer Stoffmenge, welche 1 Mol Teilchen enthält. Die Einheit der Molmasse ist g/Mol. Die Molmasse entspricht, der in g ausgedrückten Teilchenmasse eines Stoffes.
Beispiele
Berechnen der Anzahl Teilchen
Man geht dabei in drei Schritten vor:
I Bestimmen der Molmasse
II Berechnen der Anzahl Mol
III Berechnen der Anzahl Teilchen durch Multiplizieren mit der Avogadro-Zahl.
Somit wissen wir jetzt, dass in einem Papiertaschentuch 9.23 * 1019 Teilchen enthalten sind.
Molvolumen
Da es bei Gasen keinen Sinn macht, die Masse anzuschauen, benutzt man für diese das Volumen. Das Molvolumen gilt nur bei Gasen. Die zentrale Frage ist hierfür leicht abgeändert: Wieviele Teilchen sind in einem bestimmten Volumen eines Gases?
Das Volumen eines Gases ist nicht immer gleich, es ist abhängig von Druck und Temperatur. Um nicht jedesmal ein anderes Molvolumen zu bekommen, hat man sich auf Normalbedingungen (nicht zu verwechseln mit den Standardbedingungen!) geeinigt. Diese lauten wie folgt:
Druck (p) = 1,013 bar
Temperatur (T) = 0°C = 273°K
Bei diesen Bedingungen wird ein Gas als ideal bezeichnet und hat das Molvolumen von ≈ 22,4 l/mol.
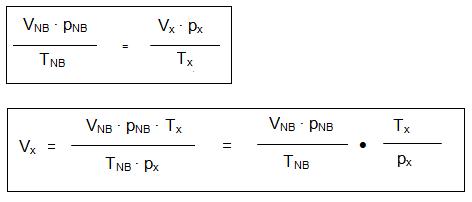
Umrechnung:
- (VNB = Volumen bei Normalbedingungen; Vx = Volumen bei jeweiliger Situation etc.)
Eine Frage stellt sich aber noch, diese lautet:
Ist die Anzahl Gasteilchen in einem bestimmten Volumen von der Art der Teilchen (Grösse / Masse) abhängig?
Saubere Überlegung;
- Kinetische Gastheorie:
Die mittlere kinetische energie hängt von der Temperatur (T) ab; sie nimmt mit der Temperatur zu.
Die Summe aller Stösse der Gasteilchen (miteinander und mit der Gefässwand) verursacht den Druck eines Gases. Je grösser die Anzahl Gasteilchen sowie die kinetische Energie der Gasteilchen, umso grösser ist der Druck und damit auch das Volumen.
Anders gesagt: Ist die Kinetische Energie von diesen Gasteilchen konstant, so ist auch die Temperatur konstant und somit auch der Platzbedarf konstant.
- Kinetische Energie = const. ⇒ Temperatur = const. ⇒ Platzbedarf = const.
In Worten gefasst kann man also sagen, dass Teilchen mit kleiner Masse zwar winziger sind, doch durch ihre erhöhte Geschwindigkeit gleich viel Platz brauchen als grosse Teilchen, welche sich langsamer fortbewegen und durch ihre Masse den gleichen Bedarf an Platz decken.
Der Satz von Avogadro

Die vorherige Erkenntnis stammte von dem italienischen Physiker und Chemiker Amadeo Avogadro, der auch die Avogadro-Zahl einführte. Sein Satz lautet wie folgt:
"Gleiche Volumen verschiedener Gase enthalten bei konstanten Bedingungen die gleiche Anzahl Teilchen."
Mit diesem Satz wurden auch die Standardbedingungen festgelegt, da man jetzt wusste, dass jedes Gas bei gleicher Temperatur und Druck das gleiche Molvolumen haben musste. Die Standardbedingungen setzen voraus, dass die Temperatur bei 25°C (298 K) und der Druck bei 1013 hPa liegen. Bei dieser speziellen Situation beträgt das Molvolumen ≈ 25l/mol.
Experimentelle Bestimmung des Molvolumens
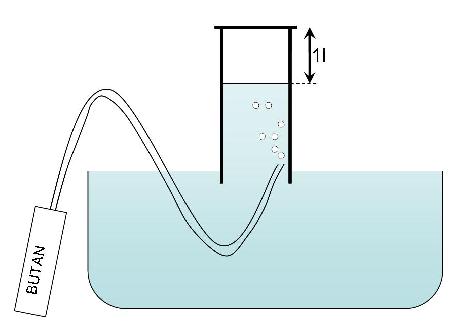
In diesem Experiment versuchen wir das Molvolumen von Butan (C4H10) aus einem Nachfüllbehälter zu bestimmen, indem wir ein mit Wasser gefülltes Glas in ein Wasserbecken tauchen, 1l Butangas hineinfliessen lassen und schliesslich mit den ermittelten Angaben das Molvolumen bestimmen. Dazu brauchen wir das in diesem Kapitel erworbene Wissen.
- Gewicht des Nachfüllbehälters: Vor dem Einflössen des Gases: 55.52g
- Nach dem Einflössen des Gases: 53.10g
Berechnen des Gewichts, welches ein Liter Butan hat:
- m (Menge des Stoffs) = 55.52g - 53.10g = 2.42g Butangas entsprechen 1l
Berechnen der Anzahl Teilchen, welche darin vorhanden sind:
- Butan C4H10: 58g = 1 mol
- 2.42g = x
- x = 0.0417 mol
- 2.42g = x
2.42g entsprechen 0.0417 mol
Bestimmen des Molvolumens von Butan:
- 0.0417 mol = 1l
- 1 mol = xl
- 1 mol =23.9l
Somit schliessen wir diese Aufgabe mit einem Molvolumen von 23.9l ab.
Quellen
- Chemieunterlagen
- Wikipedia
Weblinks
- Swisseduc – Unterrichtsserver für Chemie