Masse und Grösse der Atome: Unterschied zwischen den Versionen
(→Beispiel 3) |
K (→Beispiel 3) |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | Die Masse der Atome kann nicht mit einer Waage oder mit Hilfe der Gravitationskraft bestimmt werden, da sie zu klein zu leicht sind. Eine Alternative ist notwendig. Auf Grund der Trägheit der Atome, kann die Masse mit dem [[Massenspektrometer]] bestimmt werden. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Massenspektrometer == | == Massenspektrometer == | ||
| − | Wie kann man die Masse von Atomen bestimmen? Mit einer Waage ist dies nicht möglich, die Atome sind viel zu klein und zu leicht. | + | Wie kann man die Masse von Atomen bestimmen? Mit einer Waage oder mit Hilfe der Gravitationskraft ist dies nicht möglich, die Atome sind viel zu klein und zu leicht. |
Die Masse von Atomen wird mit einem Massenspektrometer bestimmt. | Die Masse von Atomen wird mit einem Massenspektrometer bestimmt. | ||
| − | + | [[Bild:Chemiewiki.jpg]] | |
| − | Unsere Teilchen, von welchen wir die Masse bestimmen wollen, bilden die Probe. Im linken Kasten wird diese verdampft und gelangt in den mit „Ionisierung“ beschrifteten | + | Unsere Teilchen, von welchen wir die Masse bestimmen wollen, bilden die Probe. Im linken Kasten wird diese verdampft und gelangt in den mit „Ionisierung“ beschrifteten Bereich. Durch Beschuss mit energiereichen Elektronen, werden unsere Teilchen in positiv geladene Molekül-Ionen umgewandelt, weil beim Zusammenstoß der Elektronen mit unseren Teilchen ein oder mehrere Elektronen herausgeschlagen werden. Ein Teil zerfällt aber auch in Bruchstücke. |
| − | |||
| + | Durch ein elektrisches Feld werden die Ionen beschleunigt, zu einem feinen Strahl gebündelt und durch ein Magnetfeld geschickt. Je nach Masse und Ladung werden die Ionen dort mehr oder weniger stark abgelenkt und von Detektoren aufgefangen. | ||
| + | Die höher geladenen Teilchen werden bei dieser Prozedur mehr abgelenkt, als die einfach geladenen und die Teilchen mit der geringeren Massen werden mehr abgelenkt als die mit der höheren Masse. Letzteres ist auf die Trägheit zurückzuführen. Aus den gemessenen Ablenkungswinkeln lässt sich die Masse der Teilchen sehr genau bestimmen. | ||
== Trägheit == | == Trägheit == | ||
Die Trägheit ermöglicht die Bestimmung der Masse von Atomen. (siehe [[Massenspektrometer]]) Deshalb ist sie sehr wichtig. | Die Trägheit ermöglicht die Bestimmung der Masse von Atomen. (siehe [[Massenspektrometer]]) Deshalb ist sie sehr wichtig. | ||
| − | Die Trägheit ist die Eigenschaft von Körpern, in ihrem Bewegungszustand zu verharren. | + | Die Trägheit ist die Eigenschaft von Körpern, in ihrem Bewegungszustand zu verharren. In unserem Beispiel beim Massenspektrometers ist dies die geradlinige, gleichförmige Bewegung. Wenn eine externe Kraft auf unsere geladenen Teilchen wirkt, in unserem Beispiel die Lorentzkraft (siehe Definition weiter unten), werden diese verschieden abgelenkt. |
| − | Die Gravitationskraft hat hierbei | + | |
| + | Je kleiner die Masse, je grösser die Ablenkung. Die Gravitationskraft hat hierbei kaum Einfluss auf die Ablenkung, weil die thermische Eigenbewegung der Teilchen weitaus grösser ist. | ||
| + | Dies hat zur Folge, dass die Masse der Teilchen nicht mit der Gravitationskraft bestimmt werden kann. | ||
| + | |||
| + | |||
| + | '''Definition Lorentzkraft''' | ||
| + | |||
| + | Die Lorentzkraft ist die Kraft, die auf bewegte elektrische Ladungen in elektromagnetischen Feldern wirkt. | ||
== Mol == | == Mol == | ||
| − | Durch das [[Massenspektrometer]] wurde herausgefunden, dass ein H-Atom 1.66 * 10<sup>-24</sup>g | + | Durch das [[Massenspektrometer]] wurde herausgefunden, dass ein H-Atom die Masse 1.66 * 10<sup>-24</sup>g hat. Da dies eine sehr kleine Zahl ist, definierte man eine neue Einheit – das Unit. Das heisst 1 unit = 1.66 * 10<sup>-24</sup>g. |
Daraus folgt 1g = 6.02 * 10<sup>23</sup>unit. Diese Konstante nennt man Avogadro-Zahl (NA). | Daraus folgt 1g = 6.02 * 10<sup>23</sup>unit. Diese Konstante nennt man Avogadro-Zahl (NA). | ||
| + | |||
| + | Die Bedeutung des Mols: Es ist möglich, eine definierte Anzahl an Teilchen abzuwägen. Dies ist sehr wichtig, weil chemische Reaktionen nur vollständig ablaufen, wenn die reagierenden Teilchen in einem bestimmten Stoffmengenverhältnis beteiligt sind. | ||
| + | Die Reaktionsgleichung gibt das Verhältnis der Teilchen an und mit der Molmasse kann die richtige Masse der Stoffe gewählt werden. | ||
[[Bild:Chemiewiki_2.PNG]] | [[Bild:Chemiewiki_2.PNG]] | ||
| Zeile 36: | Zeile 42: | ||
Definition Molmasse: Masse von einem Mol Teilchen (6.02 * 10<sup>23</sup> Teilchen). Die Einheit ist g/mol. | Definition Molmasse: Masse von einem Mol Teilchen (6.02 * 10<sup>23</sup> Teilchen). Die Einheit ist g/mol. | ||
| + | |||
Bestimmung der Molmasse: | Bestimmung der Molmasse: | ||
| − | Bsp. Wasser H<sub>2</sub>O → 2 H + 1 O = 2 * 1u + 1 * 16u = 18u → Molmasse = 18 g/mol | + | Bsp. Wasser H<sub>2</sub>O → 2 H + 1 O = 2 * 1u + 1 * 16u = 18u → Molmasse = 18 g/mol |
== Beispiele == | == Beispiele == | ||
| Zeile 63: | Zeile 70: | ||
''Lösungsweg:'' | ''Lösungsweg:'' | ||
| − | 1. 1 | + | 1. 1 Tropfen = 0.042g |
2. 1 Wasserteilchen H<sub>2</sub>O = 18u (Berechnung weiter oben) | 2. 1 Wasserteilchen H<sub>2</sub>O = 18u (Berechnung weiter oben) | ||
| Zeile 72: | Zeile 79: | ||
18g = 1mol | 18g = 1mol | ||
0.042g = x mol | 0.042g = x mol | ||
| − | '''x = 0. | + | '''x = 0.0023 mol''' |
5. Dreisatz für Berechnung Anzahl Teilchen | 5. Dreisatz für Berechnung Anzahl Teilchen | ||
| Zeile 87: | Zeile 94: | ||
a) Stelle die Reaktionsgleichung auf. | a) Stelle die Reaktionsgleichung auf. | ||
| − | b) Wie viele | + | b) Wie viele Wassermoleküle befinden sich in einem Liter Wasser? |
| − | c) | + | c) Was sind jeweils die Stoffmengen der beteiligten Edukte? |
d) Wie viele Gramm haben die Edukte? | d) Wie viele Gramm haben die Edukte? | ||
| Zeile 97: | Zeile 104: | ||
a) 2H<sub>2</sub> + O<sub>2</sub> → 2H<sub>2</sub>O | a) 2H<sub>2</sub> + O<sub>2</sub> → 2H<sub>2</sub>O | ||
| − | b) 1l Wasser = 1kg = 1000g | + | b) |
| + | 1l Wasser = 1kg = 1000g | ||
1 Wasserteilchen = 18u → Molmasse: 18g/mol | 1 Wasserteilchen = 18u → Molmasse: 18g/mol | ||
| + | |||
Dreisatz: | Dreisatz: | ||
18g = 1mol | 18g = 1mol | ||
| − | 1000g = | + | 1000g = x mol |
x = 55.6 mol → '''3.34 * 10<sup>25</sup> Teilchen | x = 55.6 mol → '''3.34 * 10<sup>25</sup> Teilchen | ||
| − | c) H<sub>2</sub>: 1 * 55.6mol = '''55.6mol''' | + | c) |
| + | H<sub>2</sub>: 1 * 55.6mol = '''55.6mol''' | ||
O<sub>2</sub>: 1* 55.6 = 2mol = '''27.8mol''' | O<sub>2</sub>: 1* 55.6 = 2mol = '''27.8mol''' | ||
| + | n(O<sub>2</sub>)= ½ n(H<sub>2</sub>)= 1/2∙ 55,6mol = 27,8 mol | ||
| + | |||
| + | d) | ||
| + | H<sub>2</sub>: Molmasse 1 Teilchen = 2u → 1mol = 2g | ||
| − | |||
Dreisatz: | Dreisatz: | ||
2g = 1mol | 2g = 1mol | ||
x g = 55.6mol | x g = 55.6mol | ||
'''x = 111.2g''' | '''x = 111.2g''' | ||
| + | anderer Lösungsweg: | ||
| + | n(H<sub>2</sub>) = 55,6mol; | ||
| + | M(H<sub>2</sub>) 2g/mol; | ||
| + | m(H<sub>2</sub>) = n(H <sub>2</sub>) ∙ M(H<sub>2</sub>) | ||
| + | m(H <sub>2</sub>) = 55,6mol∙ 2g/mol = 111,2g | ||
| + | |||
| + | e) | ||
| + | O<sub>2</sub>: Molmasse 1 Teilchen = 32u → 1mol = 32g | ||
| − | |||
Dreisatz: | Dreisatz: | ||
32g = 1mol | 32g = 1mol | ||
x g = 27.8mol | x g = 27.8mol | ||
'''x = 889.6g''' | '''x = 889.6g''' | ||
| + | anderer Lösungsweg: | ||
| + | n(O<sub>2</sub>)= 27,8mol; M(O<sub>2</sub>)= 32g/mol; | ||
| + | m(O<sub>2</sub>)= n(O<sub>2</sub>)∙ M(O<sub>2</sub>); | ||
| + | m(O<sub>2</sub>)= 27,8mol∙ 32g/mol = 889,6g; | ||
| + | |||
| + | == Atomgrösse == | ||
| + | |||
| + | Ein Atom besteht grundsätzlich aus einem Kern und der Hülle. | ||
| + | Im Kern befinden sich die (positiv geladenen) Protonen und die (elektrisch neutralen) Neutronen. Beide haben die Masse 1u. | ||
| + | In der Hülle befinden sich die (negativ geladenen) Elektronen. | ||
| + | |||
| + | Der Kern ist im Vergleich zur Hülle allerdings winzig klein. Die Hülle hat mit einem Durchmesser von etwa 10<sup>-10</sup>m einen ungefähr zehntausendfach größeren Durchmesser als der Kern (10<sup>-14</sup>m). Trotzdem befindet sich beinahe die ganze Masse eines Atoms in diesem Kern, da Protonen und Neutronen eine ca. 2000fach höhere Masse haben als Elektronen. | ||
| + | |||
| + | Wäre ein Atomkern so groß wie eine Stecknadel, würde das ganze Atom den Durchmesser des Eifelturmes haben. | ||
| + | |||
| + | Im Periodensystem nimmt die Atomgrösse von links nach rechts ab und von oben nach unten zu. Siehe dazu auch den Artikel [[C Das Periodensystem]] | ||
== Quellen == | == Quellen == | ||
Aktuelle Version vom 22. Juni 2010, 22:18 Uhr
Die Masse der Atome kann nicht mit einer Waage oder mit Hilfe der Gravitationskraft bestimmt werden, da sie zu klein zu leicht sind. Eine Alternative ist notwendig. Auf Grund der Trägheit der Atome, kann die Masse mit dem Massenspektrometer bestimmt werden.
Inhaltsverzeichnis
Massenspektrometer
Wie kann man die Masse von Atomen bestimmen? Mit einer Waage oder mit Hilfe der Gravitationskraft ist dies nicht möglich, die Atome sind viel zu klein und zu leicht. Die Masse von Atomen wird mit einem Massenspektrometer bestimmt.
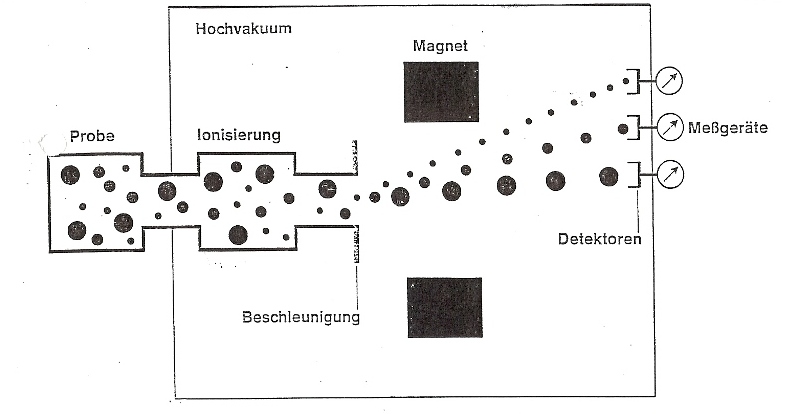
Unsere Teilchen, von welchen wir die Masse bestimmen wollen, bilden die Probe. Im linken Kasten wird diese verdampft und gelangt in den mit „Ionisierung“ beschrifteten Bereich. Durch Beschuss mit energiereichen Elektronen, werden unsere Teilchen in positiv geladene Molekül-Ionen umgewandelt, weil beim Zusammenstoß der Elektronen mit unseren Teilchen ein oder mehrere Elektronen herausgeschlagen werden. Ein Teil zerfällt aber auch in Bruchstücke.
Durch ein elektrisches Feld werden die Ionen beschleunigt, zu einem feinen Strahl gebündelt und durch ein Magnetfeld geschickt. Je nach Masse und Ladung werden die Ionen dort mehr oder weniger stark abgelenkt und von Detektoren aufgefangen. Die höher geladenen Teilchen werden bei dieser Prozedur mehr abgelenkt, als die einfach geladenen und die Teilchen mit der geringeren Massen werden mehr abgelenkt als die mit der höheren Masse. Letzteres ist auf die Trägheit zurückzuführen. Aus den gemessenen Ablenkungswinkeln lässt sich die Masse der Teilchen sehr genau bestimmen.
Trägheit
Die Trägheit ermöglicht die Bestimmung der Masse von Atomen. (siehe Massenspektrometer) Deshalb ist sie sehr wichtig. Die Trägheit ist die Eigenschaft von Körpern, in ihrem Bewegungszustand zu verharren. In unserem Beispiel beim Massenspektrometers ist dies die geradlinige, gleichförmige Bewegung. Wenn eine externe Kraft auf unsere geladenen Teilchen wirkt, in unserem Beispiel die Lorentzkraft (siehe Definition weiter unten), werden diese verschieden abgelenkt.
Je kleiner die Masse, je grösser die Ablenkung. Die Gravitationskraft hat hierbei kaum Einfluss auf die Ablenkung, weil die thermische Eigenbewegung der Teilchen weitaus grösser ist. Dies hat zur Folge, dass die Masse der Teilchen nicht mit der Gravitationskraft bestimmt werden kann.
Definition Lorentzkraft
Die Lorentzkraft ist die Kraft, die auf bewegte elektrische Ladungen in elektromagnetischen Feldern wirkt.
Mol
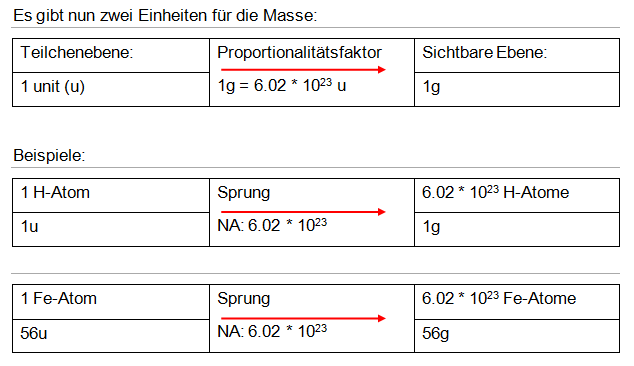
Durch das Massenspektrometer wurde herausgefunden, dass ein H-Atom die Masse 1.66 * 10-24g hat. Da dies eine sehr kleine Zahl ist, definierte man eine neue Einheit – das Unit. Das heisst 1 unit = 1.66 * 10-24g. Daraus folgt 1g = 6.02 * 1023unit. Diese Konstante nennt man Avogadro-Zahl (NA).
Die Bedeutung des Mols: Es ist möglich, eine definierte Anzahl an Teilchen abzuwägen. Dies ist sehr wichtig, weil chemische Reaktionen nur vollständig ablaufen, wenn die reagierenden Teilchen in einem bestimmten Stoffmengenverhältnis beteiligt sind. Die Reaktionsgleichung gibt das Verhältnis der Teilchen an und mit der Molmasse kann die richtige Masse der Stoffe gewählt werden.
Definition Mol: Ein Mol ist eine Anzahl von Teilchen, und zwar genau 6.02 * 1023 Teilchen. (→ keine Masse!)
Molmasse
Definition Molmasse: Masse von einem Mol Teilchen (6.02 * 1023 Teilchen). Die Einheit ist g/mol.
Bestimmung der Molmasse: Bsp. Wasser H2O → 2 H + 1 O = 2 * 1u + 1 * 16u = 18u → Molmasse = 18 g/mol
Beispiele
Beispiel 1
Aufgabenstellung:
Bestimme die Anzahl Ag-Atome in einem Silberring der Masse 2.66 g.
Lösungsweg:
1. Bestimmung der Molmasse (1 Ag = 108u → 108 g/mol)
2. Dreisatz
6.02 * 1023 Atome = 108g
x Atome = 2.66g
x = 1.5 * 1022 Atome
Beispiel 2
Aufgabenstellung:
Wie viele Teilchen hat es in einem Tropfen Wasser? Die Masse von 10 Tropfen ist 0.42 g. Gib die Lösung in mol und Anzahl Teilchen an.
Lösungsweg:
1. 1 Tropfen = 0.042g
2. 1 Wasserteilchen H2O = 18u (Berechnung weiter oben)
3. → Molmasse = 18g/mol
4. Dreisatz für Berechnung mol
18g = 1mol
0.042g = x mol
x = 0.0023 mol
5. Dreisatz für Berechnung Anzahl Teilchen
1mol = 6.02 * 1023 Teilchen
0.0023mol = x Teilchen
x = 1.4 * 1021 Teilchen
Beispiel 3
Synthese von Wasser aus den Elementen
Aufgabenstellung:
a) Stelle die Reaktionsgleichung auf.
b) Wie viele Wassermoleküle befinden sich in einem Liter Wasser?
c) Was sind jeweils die Stoffmengen der beteiligten Edukte?
d) Wie viele Gramm haben die Edukte?
Lösungsweg:
a) 2H2 + O2 → 2H2O
b)
1l Wasser = 1kg = 1000g
1 Wasserteilchen = 18u → Molmasse: 18g/mol
Dreisatz:
18g = 1mol
1000g = x mol
x = 55.6 mol → 3.34 * 1025 Teilchen
c)
H2: 1 * 55.6mol = 55.6mol
O2: 1* 55.6 = 2mol = 27.8mol
n(O2)= ½ n(H2)= 1/2∙ 55,6mol = 27,8 mol
d)
H2: Molmasse 1 Teilchen = 2u → 1mol = 2g
Dreisatz:
2g = 1mol
x g = 55.6mol
x = 111.2g
anderer Lösungsweg:
n(H2) = 55,6mol;
M(H2) 2g/mol;
m(H2) = n(H 2) ∙ M(H2)
m(H 2) = 55,6mol∙ 2g/mol = 111,2g
e)
O2: Molmasse 1 Teilchen = 32u → 1mol = 32g
Dreisatz:
32g = 1mol
x g = 27.8mol
x = 889.6g
anderer Lösungsweg:
n(O2)= 27,8mol; M(O2)= 32g/mol;
m(O2)= n(O2)∙ M(O2);
m(O2)= 27,8mol∙ 32g/mol = 889,6g;
Atomgrösse
Ein Atom besteht grundsätzlich aus einem Kern und der Hülle. Im Kern befinden sich die (positiv geladenen) Protonen und die (elektrisch neutralen) Neutronen. Beide haben die Masse 1u. In der Hülle befinden sich die (negativ geladenen) Elektronen.
Der Kern ist im Vergleich zur Hülle allerdings winzig klein. Die Hülle hat mit einem Durchmesser von etwa 10-10m einen ungefähr zehntausendfach größeren Durchmesser als der Kern (10-14m). Trotzdem befindet sich beinahe die ganze Masse eines Atoms in diesem Kern, da Protonen und Neutronen eine ca. 2000fach höhere Masse haben als Elektronen.
Wäre ein Atomkern so groß wie eine Stecknadel, würde das ganze Atom den Durchmesser des Eifelturmes haben.
Im Periodensystem nimmt die Atomgrösse von links nach rechts ab und von oben nach unten zu. Siehe dazu auch den Artikel C Das Periodensystem
Quellen
- Chemieunterlagen Herr Deuber